Reverse-Z 역 깊이 버퍼의 깊이 정밀도 차이

https://developer.nvidia.com/content/depth-precision-visualized

Depth Precision Visualized

https://tomhultonharrop.com/mathematics/graphics/2023/08/06/reverse-z.html

Reverse Z (and why it’s so awesome)

GPU에서 사용하는 깊이 버퍼는 보통 부동 소수점 형식을 사용하여 깊이 값을 저장한다. 부동 소수점 형식은 수의 크기에 따라 가변적인 정밀도를 제공하는데, 이는 깊이 값을 표현하는 데 있어 몇 가지 중요한 영향을 미칠 수가 있다.

부동 소수점 깊이 버퍼

https://courses.engr.illinois.edu/cs357/fa2019/references/ref-1-fp/

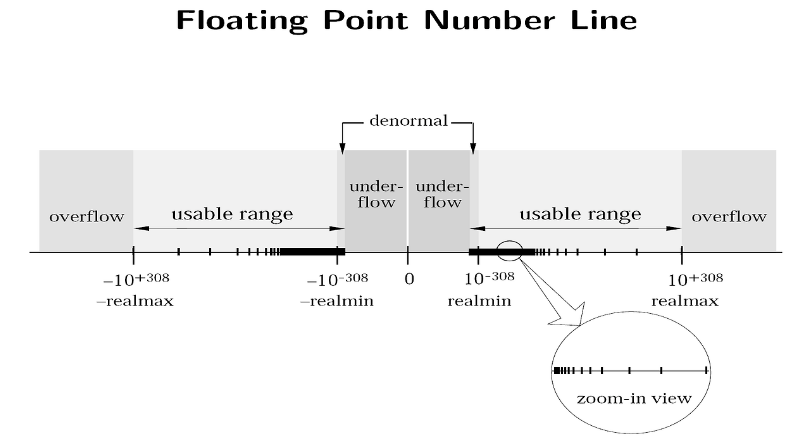
부동 소수점 숫자는 유효 숫자(Significand)와 지수(Exponent)로 구성된다. 작은 숫자는 더 많은 정밀도를 가지지만, 큰 숫자는 상대적으로 적은 정밀도를 가진다.
( 0.0과 1.0 사이의 전체 범위 중에서 표현 가능한 모든 값의 약 0.79% 만이 0.5와 1.0 사이에 있고, 0.0과 0.5 사이에는 무려 99.21% 가 있다는 것을 알 수 있다 )

카메라 근처의 깊이 값은 더 작은 숫자로 표현되고, 먼 거리의 깊이 값은 더 큰 숫자로 표현된다.

역 Z 매핑

깊이 값을 역순으로 저장하여, 깊이 값이 클수록 카메라에 가까운 객체로 매핑합니다. 즉, 근접 평면의 깊이 값을 더 큰 숫자로, 먼 평면의 깊이 값을 더 작은 숫자로 저장한다.
( 투영 행렬을 계산 할 때 near 평면과 far 평면의 값을 바꿔서 적용한다. 그리고 깊이 비교 함수를 맞게 변경이 필요하다.)

근접 평면에서 먼 평면으로 갈수록 정밀도가 일정하게 분포된다. 부동 소수점 형식에서는 작은 숫자가 더 많은 정밀도를 가지기 때문에, 역 Z 매핑은 먼 거리의 객체에도 높은 정밀도를 제공한다. 역 Z 매핑은 부동 소수점의 가변 정밀도 특성을 최대한 활용하여 깊이 버퍼의 정밀도를 균형 있게 분배한다. 이는 Z 파이팅 현상을 줄이고, 전체적인 그래픽 품질을 높이는 데 기여한다.

결론적으로, 역 Z 매핑은 깊이 버퍼의 정밀도를 향상시켜 그래픽 렌더링의 품질을 높이는 중요한 기술이다. 이는 특히 부동 소수점 깊이 버퍼의 특성을 최대한 활용하여, 근접 객체뿐만 아니라 먼 거리의 객체도 높은 정밀도로 표현할 수 있게 한다.